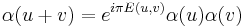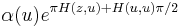Appell–Humbert theorem
In mathematics, the Appell–Humbert theorem describes the line bundles on a complex torus or complex abelian variety. It was proved for 2-dimensional tori by Appell (1891) and Humbert (1893), and in general by Lefschetz (1921)
Statement
Suppose that T is a complex torus given by V/U where U is a lattice in a complex vector space V. If H is a Hermitian form on V whose imaginary part is integral on U×U, and α is a map from U to the unit circle such that
then
is a 1-cocycle on U defining a line bundle on T.
The Appell–Humbert theorem (Mumford 2008) says that every line bundle on T can be constructed like this for a unique choice of H and α satisfying the conditions above.
Ample line bundles
Lefschetz proved that the line bundle L, associated to the Hermitian form H is ample if and only if H is positive definite, and in this case L3 is very ample. A consequence is that the complex torus is algebraic if and only if there is a positive definite Hermitian form whose imaginary part is integral on E×E.
References
- Appell, P. (1891), "Sur les functiones périodiques de deux variables", J. de math Sér IV 7: 157–219, http://gallica.bnf.fr/ark:/12148/bpt6k107455z.image.f159.langFR
- Humbert, G. (1893), "Théorie générale des surfaces hyperelliptiques", J. de math Sér IV 9: 29–170, 361–475, http://gallica.bnf.fr/ark:/12148/bpt6k107457q.image.f29.langFR
- Lefschetz, Solomon (1921), "On Certain Numerical Invariants of Algebraic Varieties with Application to Abelian Varieties", Transactions of the American Mathematical Society (Providence, R.I.: American Mathematical Society) 22 (3): 327–406, ISSN 0002-9947, http://www.jstor.org/stable/1988897
- Lefschetz, Solomon (1921), "On Certain Numerical Invariants of Algebraic Varieties with Application to Abelian Varieties", Transactions of the American Mathematical Society (Providence, R.I.: American Mathematical Society) 22 (4): 407–482, ISSN 0002-9947, http://www.jstor.org/stable/1988964
- Mumford, David (2008) [1970], Abelian varieties, Tata Institute of Fundamental Research Studies in Mathematics, 5, Providence, R.I.: American Mathematical Society, ISBN 9788185931869, MR0282985, OCLC 138290